One of the most popular math equation puzzles on social media is interesting because it doesn’t have one correct answer and it illustrates the nature of a solution divergence.

Here is an example. The following two problems can be solved correctly regardless if we use sum of the digits in the product or product of the sum of digits methods:

Set 1: 11×11=4
Set 2: 22×22=16
Set 3: 33×33=?

For first set
Method 1   11×11=121 then summing the digits in the products give us 1+2+1=4
Method 2   (1+1) x (1+1) = 4

and for second set
Method 1  22×22=484 then summing the digits in the product gives us 4+8+4=16
Method 2  (2+2) x (2+2) = 16

But when it comes to the next set of 33×33=? each solution diverges and will yield two different results (see result bellow for method 1 and 2).

Method 1 (sum of the digits in the product) it is: 33×33=18

33×33=1089 or 1+0+8+9= 18

Method 2 (product of the sum of digits) it is: 33×33=36

(3+3) x (3+3) = (6) x (6)=36

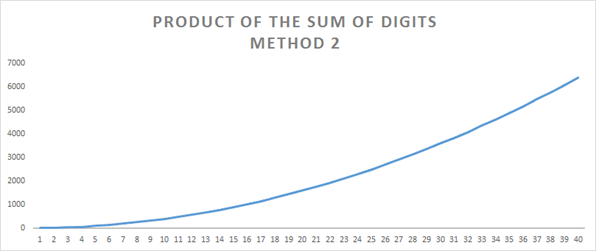
Here is a graphic solution for method 2

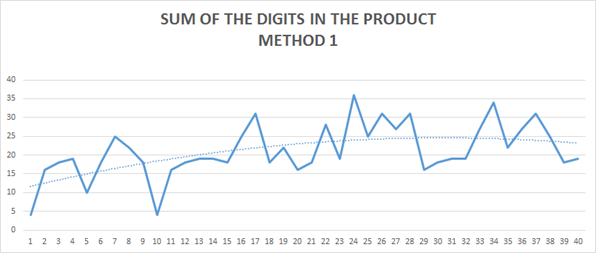
Here are the solution for the first 40 sets for each method.

Method 1				Method 2
11	11	121	4	11	11	4
22	22	484	16	22	22	16
33	33	1089	18	33	33	36
44	44	1936	19	44	44	64
55	55	3025	10	55	55	100
66	66	4356	18	66	66	144
77	77	5929	25	77	77	196
88	88	7744	22	88	88	256
99	99	9801	18	99	99	324
110	110	12100	4	110	110	400
121	121	14641	16	121	121	484
132	132	17424	18	132	132	576
143	143	20449	19	143	143	676
154	154	23716	19	154	154	784
165	165	27225	18	165	165	900
176	176	30976	25	176	176	1024
187	187	34969	31	187	187	1156
198	198	39204	18	198	198	1296
209	209	43681	22	209	209	1444
220	220	48400	16	220	220	1600
231	231	53361	18	231	231	1764
242	242	58564	28	242	242	1936
253	253	64009	19	253	253	2116
264	264	69696	36	264	264	2304
275	275	75625	25	275	275	2500
286	286	81796	31	286	286	2704
297	297	88209	27	297	297	2916
308	308	94864	31	308	308	3136
319	319	101761	16	319	319	3364
330	330	108900	18	330	330	3600
341	341	116281	19	341	341	3844
352	352	123904	19	352	352	4096
363	363	131769	27	363	363	4356
374	374	139876	34	374	374	4624
385	385	148225	22	385	385	4900
396	396	156816	27	396	396	5184
407	407	165649	31	407	407	5476
418	418	174724	25	418	418	5776
429	429	184041	18	429	429	6084
440	440	193600	19	440	440	6400

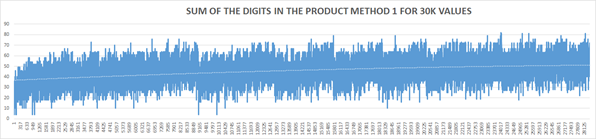
It is interesting to note the series growth patterns for each method.  Where in method 1, the values tend to cluster around a range of several values (see pattern for 30K solutions), in method 2 the growth is polynomial.

 

© Copyright 2017 Yaacov Apelbaum, All Rights Reserved.